そこで,定積分を求めるときは,計算が最も楽になるように C=0 とする. ⇒ 定積分の計算では,原始関数の内で C=0 の場合を使う 1 多項式,分数関数,無理関数 不定積分の公式のまとめ α が実数で, −1 以外のとき ∫wn x α dx= xα1 α1nnn C (11)文字式の足し算・引き算は同類項でなければいけませんが、分数の場合は 分母・分子がどちらも同類項の場合にしか計算はできません 。 ① 02 x 07 x = 09 x多項式の計算と係数 多項式の計算をする前に、係数と同類項の意味を理解しましょう。係数とは、単項式の数の部分です。3aの係数は「3」、xの係数は「1」です。 同類項とは、多項式中の文字が同じ項です。下記の多項式の同類項を見つけてください。 3abx2a

文字式 カッコや分数を含んだ多項式 の計算方法 数学fun
多項式の計算 分数
多項式の計算 分数-多項式 ,有理式 部分分数分解を計算する: (x^24)/(x^4x) の部分分数 More examples ブール簡約同類項をまとめる 多項式の加法・減法 縦の計算 多項式と数の乗法除法 分配法則と加法減法 分数形の加法・減法 乗法 累乗 除法1(整数) 除法2(分数) 乗法と除法の混ざった計算 式の値 式による説明(2つの連続する奇数・・・) 式による説明(2けたの自然数・・・) 式による説明(奇数と奇数の和・・・) 式による説明(各位の数の和が9の倍数・・・) 式による説明(3で割ると1




多項式と単項式の乗除 無料で使える中学学習プリント
多項式 は x n (n は0以上の整数) の形の式の定数倍・和・差なので、左の (I)の公式でαに0以上の整数をあてはめると求められる。係数の求め方、計算 色々な式の係数を求めましょう。 上式のように、単項式の和で表す式を多項式といいます。まず、多項式を単項式に分けます。 ですね。係数とは単項式の数の部分です。よって、係数はそれぞれ 「3、6、1」 です。分子の(多項式)は( )でくくってしまいます。 分数の分母、分子に多項式がある時は、いつも(括弧)があると考えます。 分数-分数 と見て、通分します。分母は2と3だから、 6に揃えます 分母は6に揃え、分子はまだ計算しません。
19/2/21 多項式とは \(2\) つ以上の項で構成された式、つまり、 複数の項を足し算でつなげた式 のことです。 \(\displaystyle 3 \color{salmon}{} 3x \color{salmon}{} \frac{x}{3}多項式と分数式を合わせて, 有理式(rational expression) という. 分数式では,普通の分数と同じように,分母,分子に 0 以外の同じ式をかけてもよいし, 分母,分子に共通な因数で割ってもよい.3/8/17 上野竜生です。文系で最後のほうに習う微分積分(多項式)ですが、意外と簡単です。しかし計算を面倒臭がって使ってはいけない公式を使ってしまう人もいます。そんな落とし穴を紹介していきます。 基本の公式 ・\( f
指数 (累乗)の計算は、分母・分子間で指数の差を求める。 多項式を単項式で割る場合には、下のように計算する 多項式を整数で割った分数どうしの加法・減法は、通分を行ってから同類項間の加減を行う。 多項式の展開を行う際に、符号にはくれぐれも注意する。 平方根を含む分数では、平方根どうし、整数どうしはそれぞれ約分可能である。 分母に平方根が 2数 分数を含む多項式の計算 Youtube 今回は中2で学習する式の計算の単元から 単項式多項式がそれぞれ何次式になるのか 係数や次数ってなに 中学数学 中学生に伝えたい数学を勉強する3つのコツ 中3数学 1646 中3数学因数分解とはな更新日時 ので整式(単項式)ではありません(ちなみに,整式÷整式 で表せる式を有理式,または分数式と言います。



中2 式の計算6 動画 多項式の除法 わり算 発展の解説 中学数学の勉強に




単項式の全てがこれでわかる 単項式の係数と次数 乗法 除法や多項式との違いまで 高校生向け受験応援メディア 受験のミカタ
1年 文字式の計算2(加減)3③答 17 a → − 17 a 2年 角度2 3③130°→131° 3年 放物線と図形1 5(3)解答(0,4)→(0,4)または(0,4) 1年 文字式の計算3(乗除) 答3③9c誤→49c正 1年 文章を等式にする 答(9)12x→ 9 2 x 1年 方程式計算4 ⑪右辺5/6→5/6x文字式(カッコや分数を含んだ多項式)の計算方法 管理人 12月 18, 18 / 6月 19, 中学校数学の序盤で習う文字式の計算は今後あらゆる分野の基盤となる概念なので、これをしっかり抑えておくのはとても重要です。多項式の積の展開がわからない方は、こちらのページを見てみてください! →中3数学多項式を展開するときの4つの便利な公式を覚えよう! 次の式を因数分解してみよう。 \(xy4y=(x4)y\)




中学2年生 数学 式の計算 多項式の計算 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中2 数学 1 6 多項式の計算 分数 Youtube
13/5/19 多項式と単項式の乗除 基本的な式の展開の練習問題プリントです。 正確に計算出来るように練習してください。 *画像をクリックするとpdfファイルをダウンロード出来ます。 単項式と多項式の乗除 順番に計算します。 分数の割り算は逆数にしてかけ算にいろいろな多項式の計算について解説します。 このように ( )の前の数字5を ( )の中の項に順にかけて計算していきます。 このように( )の中の項を順番に2でわっていきます。 このように多項式を分数でわるときは、かけ算の式に直して計算します同様にして、 −1a のように係数が −1 のときは省略して −a と表されるので、 −a の係数は −1 です。 例 2 a → 係数は 2 −3 xy 2 → 係数は −3 x → 係数は 1 単項式で掛けられている文字の個数をその単項式の 次数 といいます。 文字の部分 ではなく、 文字の個数 が次数であることに注意しましょう。 例 2 a → 次数は 1



3




多項式の掛け算 割り算と分配法則 代入計算のやり方 リョースケ大学
30/1/ 単項式と多項式 加法・減法 分数型 単項式の乗除 乗除混合 等式の変形 式の説明① 式の説明②まずは計算するためのポイントを確認しましょう。 POINT ① 通分する(分母をそろえる) ↓ POINT ② 分数を $\textcolor{blue}{1}$ つにする ↓ POINT ③ (マイナスは符号注意) ↓ POINT ④ 同類項をまとめる(約分できるときは忘れずに) 問題で確認しましょう。テスト頻出問題をダウンロード ※基本編とほとんど同じhttps//ecommonsbiz/wpcontent/uploads//06/DB0pdf 動画リンク 同類項と多項式の計算(基礎)https



2




多項式の計算応用 分数をふくむ式 教遊者
分数の計算はテストや入試には出題されやすいんですよね。 でも、ミスしてしまう人も多い。 それならば! 自分が正解すれば、ライバルたちと差をつけることができる! そう考えたら、文字式の分数問題ってすっごく重要だよね。 さぁ、練習あるのみだ!Enjoy the videos and music you love, upload original content, and share it all with friends, family, and the world on21/6/ 多項式の計算 数×多項式、多項式×数は分配法則で計算します。 〈具体例〉 3(3x5y) =3×3x3×5y =9x15y −2(4a−9b) =−2×4a(−2)×(−9b) =−8a18b (−5x−2y)×4 =(−5x)×4(−2y)×4 =−x−8y (7ab)×(−6) =7a×(−6)b×(−6) =−42a−6b 多項式÷数も分配法則の考え方です。
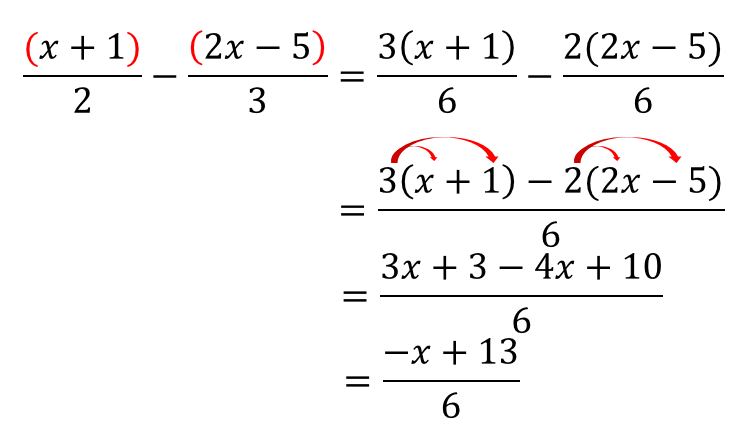



文字式 分数の計算問題を1から丁寧に 数スタ



2
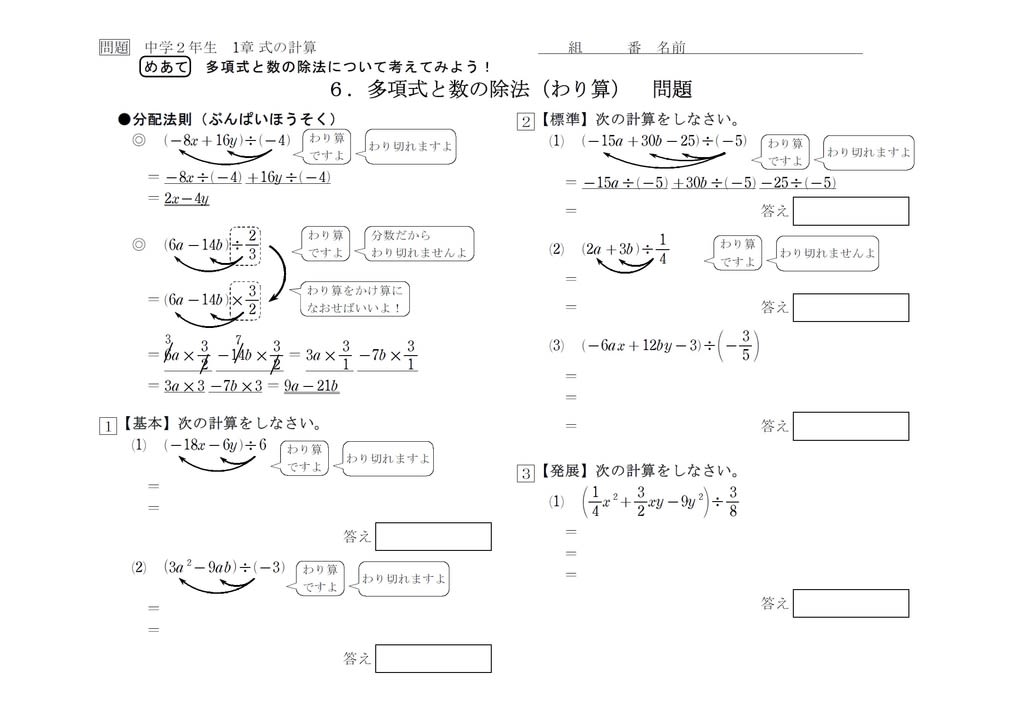
単項式の除法 式の計算練習問題に挑戦しよう! 式の計算まとめ! 中3受験生へこの力を身につけたら本番で60点は楽勝にとれる!1章 式の計算 1節 式の計算 ② 多項式の計算(1) 今回の目標 分数が混じっている計算ができるようになる。 ※中1の内容よりも分数の問題の比率が上がっています。 下の青い文字をクリックしてください。 問題・解答・解説のpdfファイルが開きます。 多項式の計算 なんだか文字が多くてややこしいの というわけで、今回の記事では中2で学習する 「多項式の計算」 についてイチから解き方を確認していきましょう。



2



2
28/5/18 ここでの内容は、こんな人に向けて書いています 多項式の掛け算や割り算のやり方がわからない 多項式に分配法則を使って計算する方法が知りたい 多項式を解く計算手順を復習したい このページでは、多項式と数の乗法(掛け算)と除法(割り算)の計算方法を紹介しています。 次のような下記の方程式では、元々、xは左辺にあります。よって、数を右辺に移項します。答えは x4=-5 x=-5-4 x=-9 です。 移項と分数の関係 分数の項があるとややこしく感じますが、移項の方法は同じです。下記の方程式を解きましょう。 です。そうすれば、多項式の足し算と引き算での計算ミスを防げるようになります。 練習問題:単項式と多項式の足し算と引き算 Q1 次の計算をしましょう $2a÷(5)$ $3b÷2x÷y$ A1 解答 単項式の計算では、割り算を掛け算に直さなければいけません。
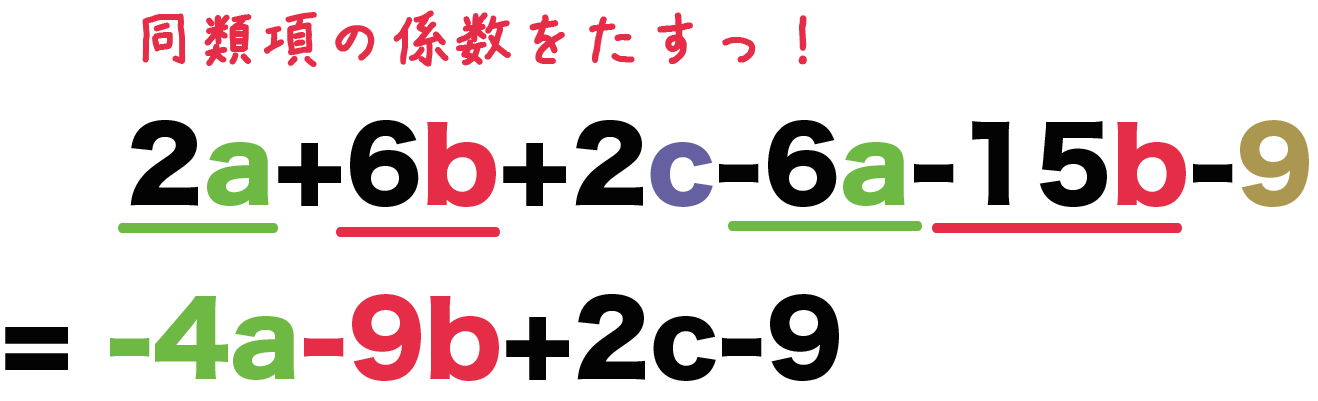



中2数学 多項式の計算問題を瞬殺できる3つのステップ Qikeru 学びを楽しくわかりやすく




文字式 カッコや分数を含んだ多項式 の計算方法 数学fun
文字式の計算(カッコ、分数を含む多項式)計算ドリル/問題集 中学校1年の数学で習う「文字式の計算」を身につけるための問題集です。 カッコや分数を含む多項式の問題なので、分配法則を用いた計算、符号の反転などに慣れるのに役立つでしょう。 問題の数値はランダムで生成することができ、答えの表示・非表示も切り替えられます。 印刷してご活用多項式 多項式を調べ,定義域と値域,次数,根,プロット,判別式等の特性を計算する. 多項式の特性を計算する: x^4 4x^3 8x 1 複数の変数を持つ多項式の特性を計算する: x^3 x^2 y x y^2 y^3 多項式の次数を求める: (x2)^5 (x2)^5の次数 多項式の最大公約数を求める:8/8/21 今回は「多項式」に「数」を「かけたり・わったり」して計算をする問題です 基本のやり方は、前回学習した内容と同じです 分配法則や式の値なども使っていきます では一緒にやっていきま



数学多項式の計算分数を含む式の計算 計算ミスをしていて 自分で Yahoo 知恵袋




中学2年生 数学 式の計算 多項式の計算 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




S計算 部分分数分解編 おいしい数学



2



いろいろな多項式の計算の分数をふくむ式の計算について質問がありま Yahoo 知恵袋




中学2年数学 式の計算 多項式と数の乗法 掛け算 除法 割り算 分配法則を使って計算しよう 数学の面白いこと 役に立つことをまとめたサイト




スタディピア 数と式




多項式の掛け算 割り算と分配法則 代入計算のやり方 リョースケ大学




中学2年数学 式の計算 多項式と数の乗法 掛け算 除法 割り算 分配法則を使って計算しよう 数学の面白いこと 役に立つことをまとめたサイト
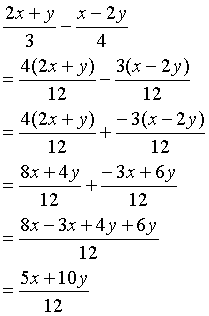



分数の復習と分数式の計算




分数の文字式と整数の掛け算 よく使う非常に大切な知識 中学や高校の数学の計算問題



いろいろな多項式の計算の分数をふくむ式の計算について質問がありま Yahoo 知恵袋



Www City Funabashi Lg Jp Gakkou 0002 Asahi J 0003 P0798 D Fil 2 1 Pdf
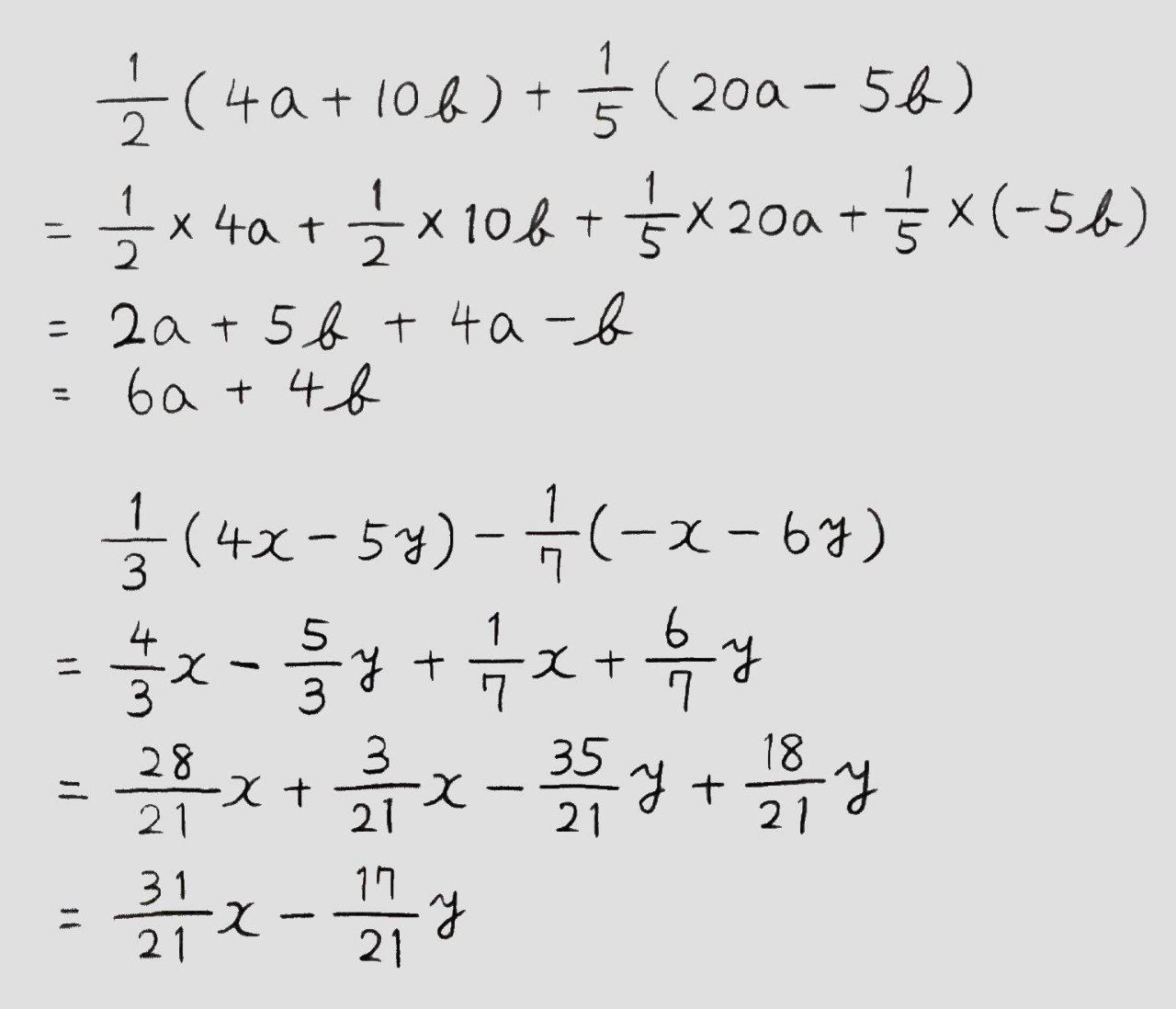



忙しい人のための中学数学 式の計算 計算ルール編 桜花 現役バイト塾講師 Note




単項式と多項式の違い 簡単な問題を解けば違いがわかる 中学や高校の数学の計算問題




多項式の分数の計算 数学2年 塾の先生が作った本当に欲しいプリント 楽天ブログ




部分分数分解の主要パターン おいしい数学




多項式の計算応用 分数をふくむ式 教遊者




文字式 代数式 のルールと単項式 多項式の足し算と引き算 リョースケ大学




中2数学 式の計算 多項式の分数計算 Youtube




中学数学 多項式 の教え方 展開の基本
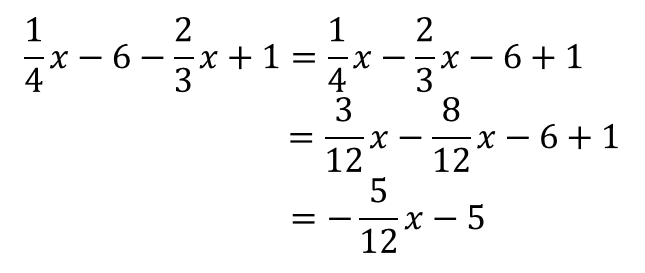



文字式 分数の計算問題を1から丁寧に 数スタ




数学中2 多項式の計算3 Clear




多項式と単項式の乗法 除法 教遊者




中学数学2年 単項式の乗法と除法 受験の月



1




中3 展開と因数分解2 多項式と単項式の除法 予習 中学数学の勉強に




多項式と単項式の乗除 無料で使える中学学習プリント




分数 分数がある式の計算 中学生からの勉強質問 数学 進研ゼミ中学講座




分数を含む多項式を理解しよう 数学嫌いな子のための簡単理解法 分かりにくいを分かりやすいに




2数 分数を含む多項式の計算 Youtube




式の計算 単項式の乗法と除法計算のポイント 文字の約分 中学数学をはじめから分かりやすく



2




中3 展開と因数分解2 多項式と単項式の除法 予習 中学数学の勉強に




中2数学 多項式の乗法 かけ算 例題編 映像授業のtry It トライイット
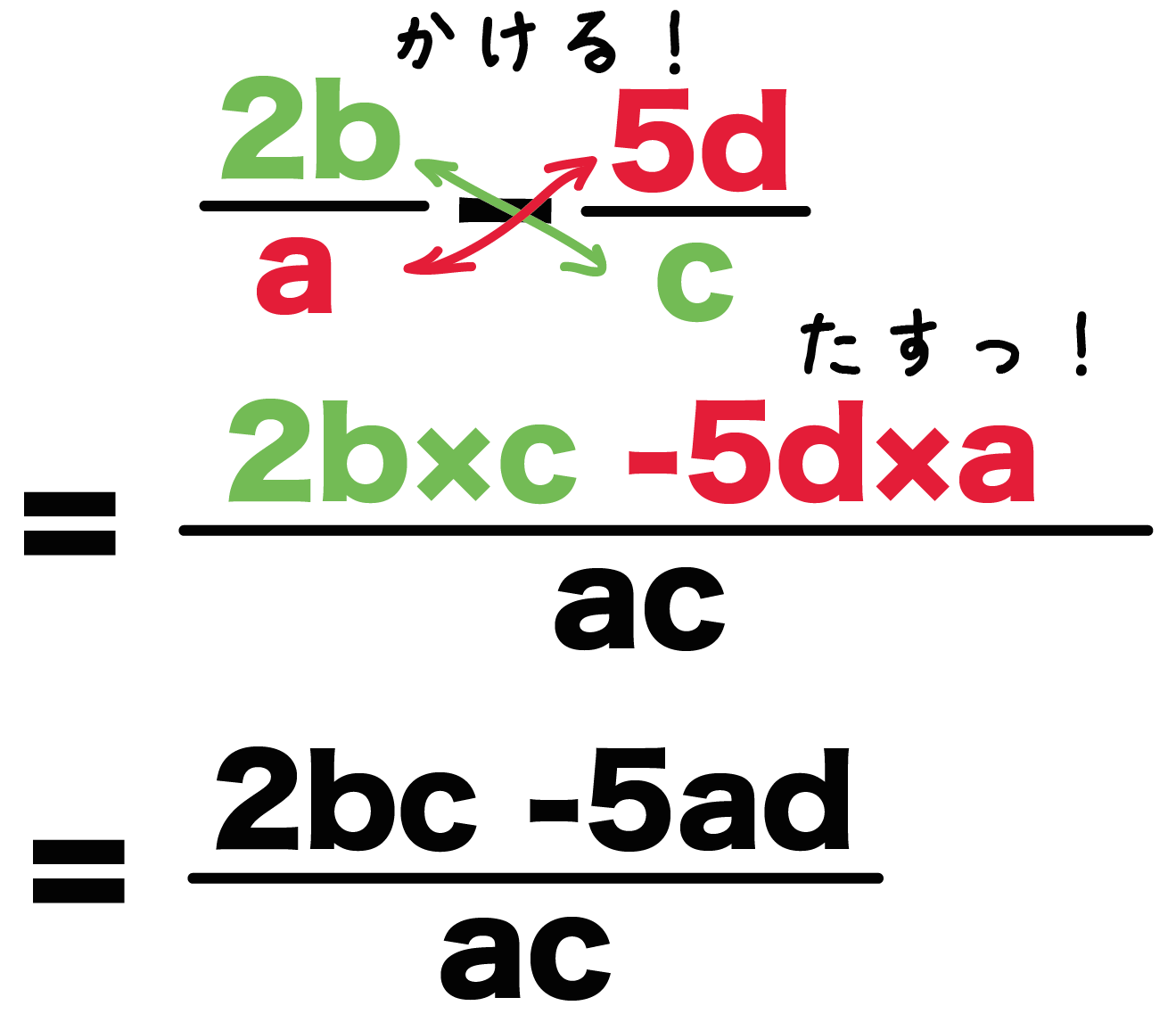



3分でわかる 分数の文字式の通分方法 Qikeru 学びを楽しくわかりやすく




モノマナビ研究所




文字式 カッコや分数を含んだ多項式 の計算方法 数学fun




分数の方程式の問題 解き方のコツは両辺に数をかけて分母を消せ 中学や高校の数学の計算問題
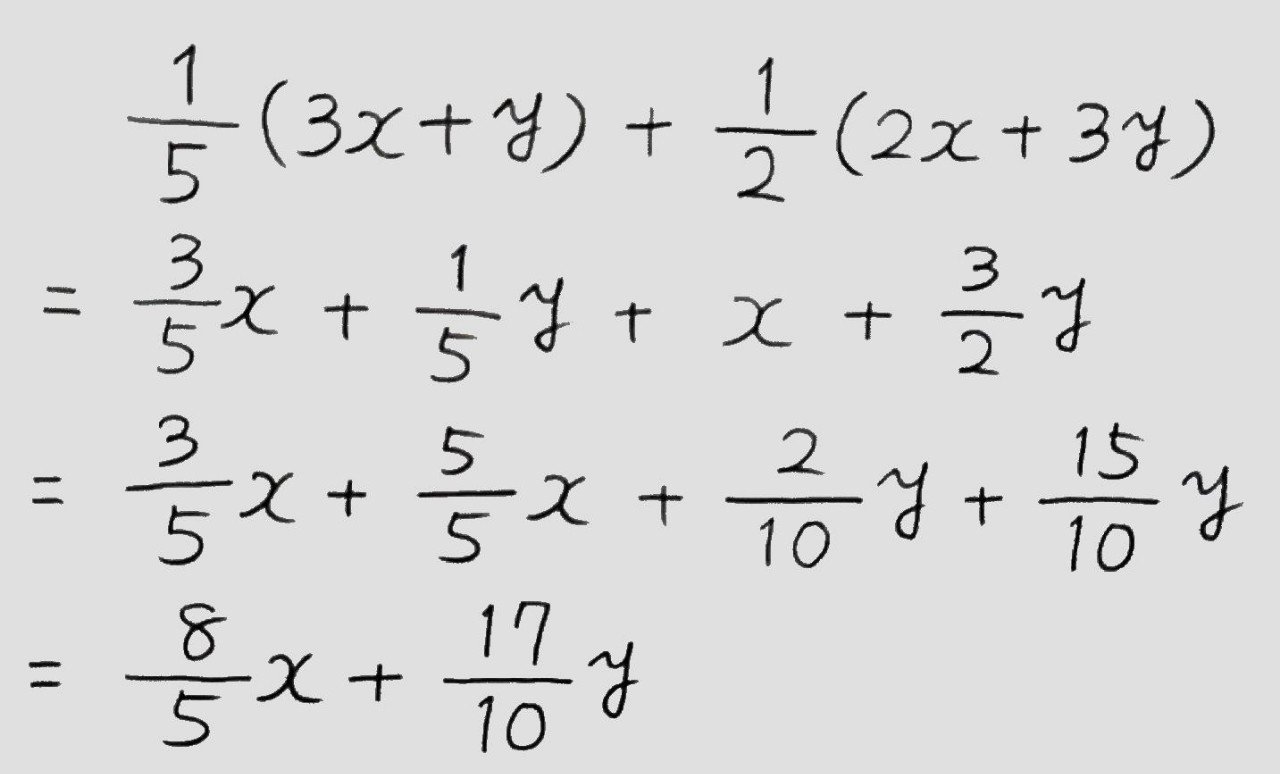



忙しい人のための中学数学 式の計算 計算ルール編 桜花 現役バイト塾講師 Note
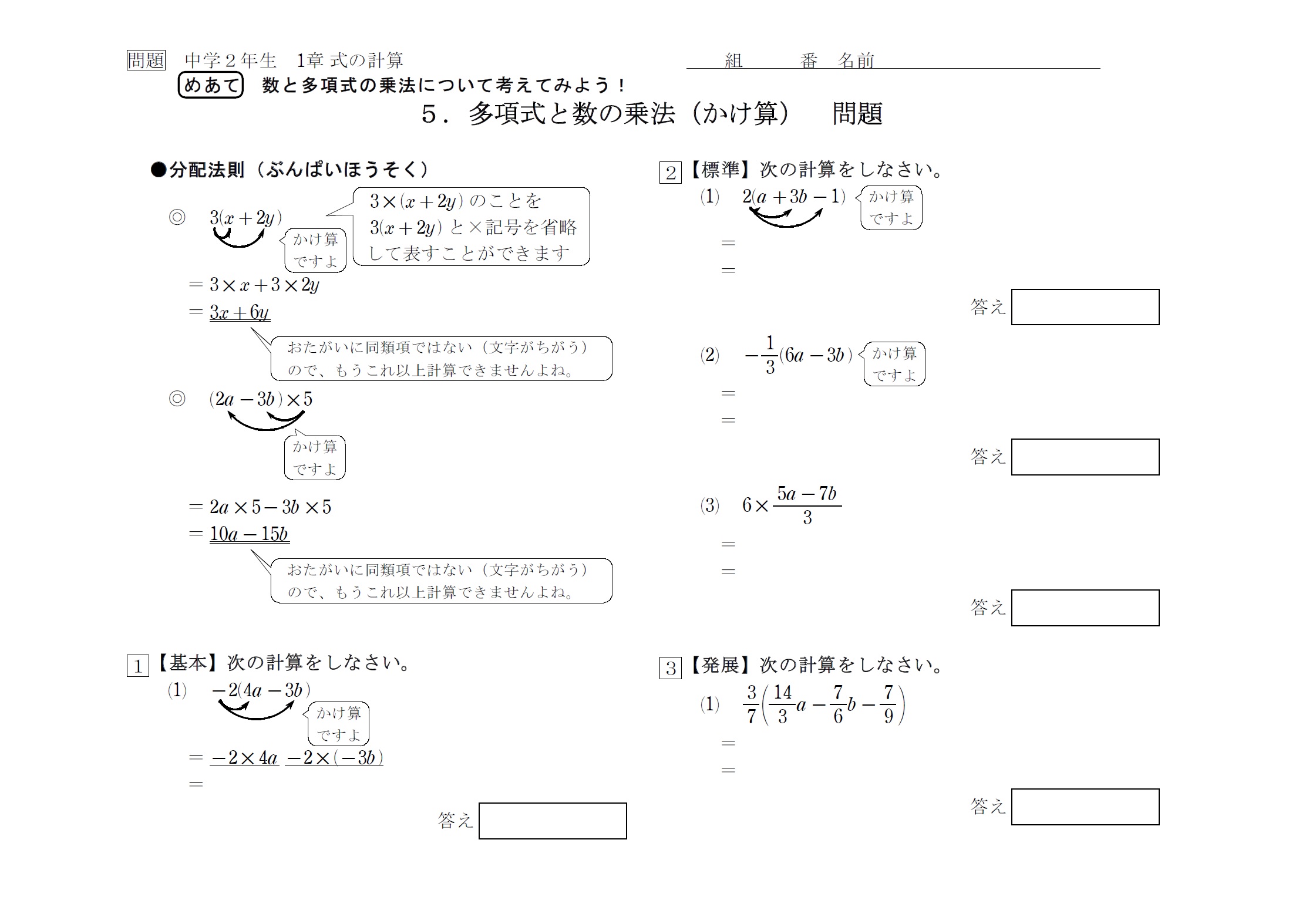



ますまち プリントを作りました 内容は中学2年 式の計算 の 多項式の乗法 かけ算 です 基本の計算は難しくありませんが マイナスや分数が出てきたときに間違えがおきやすいです 数学 中学数学 中学生 中学2年生 中2 中2数学 勉強 勉強垢




中学2年生 数学 式の計算 多項式の計算 問題プリント 無料ダウンロード 印刷 このページの問題プリント 全部




単項式




小学3年生 算数 無料問題集 分母が同じ分数の足し算 おかわりドリル




中学2年数学 式の計算 単項式と多項式とは その次数と係数もマスターしよう 数学の面白いこと 役に立つことをまとめたサイト




数学 中2 4 いろいろな多項式の計算 Youtube




中3 中3 数学 多項式の計算 式の乗法 除法 中学生 数学のノート Clear




文字式 カッコや分数を含んだ多項式 の計算方法 数学fun




中学2年数学 分数形の加法と減法 勉強 Youtube スタディチューブ




文字式 カッコや分数を含んだ多項式 の計算方法 数学fun




中2数学 式の計算 多項式の分数計算 Youtube
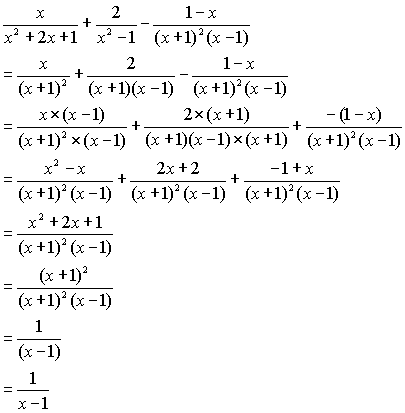



分数の復習と分数式の計算
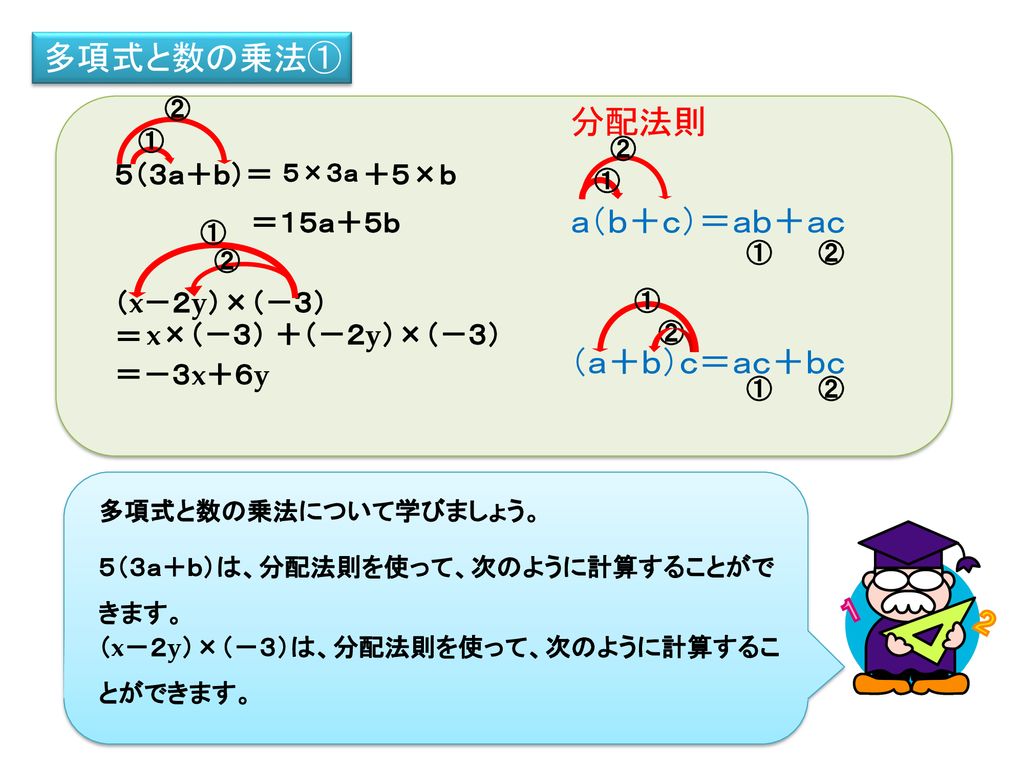



多項式と数の乗法 除法について学ぼう Ppt Download




式の計算 多項式の乗法と除法の計算の解き方とは は に変えて後ろの数を逆数にする 中学数学をはじめから分かりやすく




分数 分数の約分 中学生からの勉強質問 数学 進研ゼミ中学講座




分母が違う分数の足し算 通分して計算する理由は分配法則を考えればわかる 数学の面白いこと 役に立つことをまとめたサイト



分数 文字式 約分




多項式の計算 チーム エン




多項式と単項式の乗除 無料で使える中学学習プリント



1
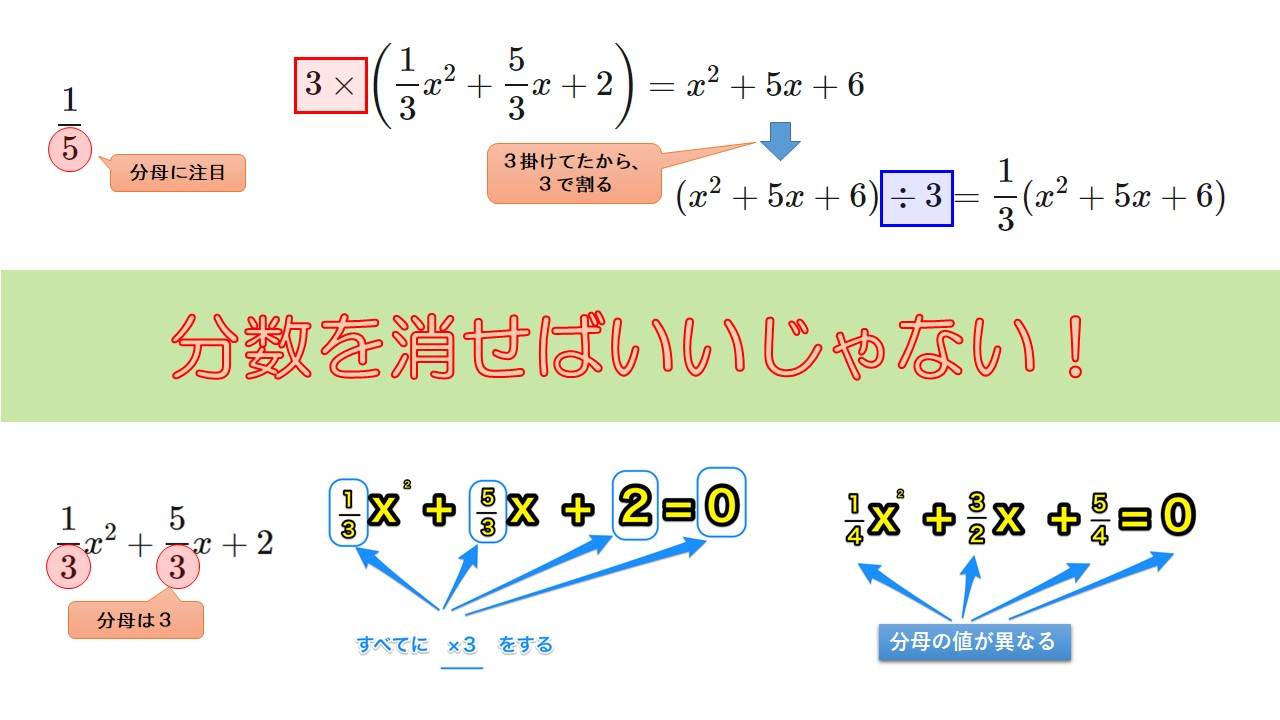



高校数学 因数分解 分数が登場する式を因数分解する方法 わかりやすく解説します 数学の面白いこと 役に立つことをまとめたサイト



Q Tbn And9gcrkz55leutoiyzt5r9bugl3exoxymmqopzocnnxi6kwx2peohab Usqp Cau



分数 文字式 約分




文字式の筆算のやり方を解説 多項式の加法 減法 数スタ
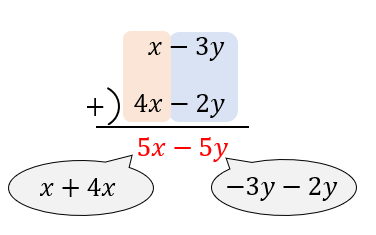



中2数学 多項式の計算のやり方についてイチから解説 中学数学 理科の学習まとめサイト




中1数学 文字式の計算に自信はありますか 単項式 多項式の計算 文字式の計算 の解き方 教え方 いっしょに勉強しよ
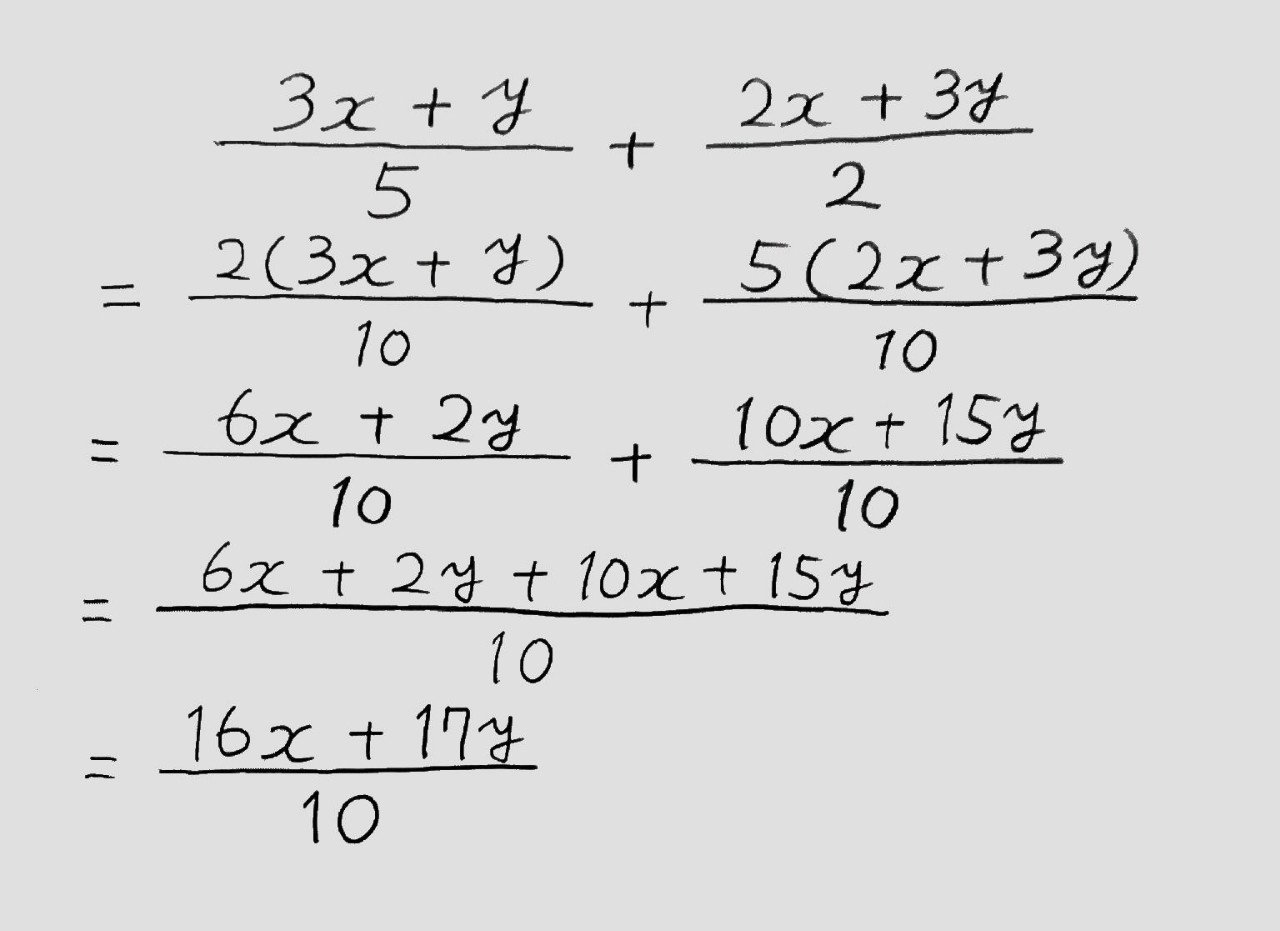



忙しい人のための中学数学 式の計算 計算ルール編 桜花 現役バイト塾講師 Note
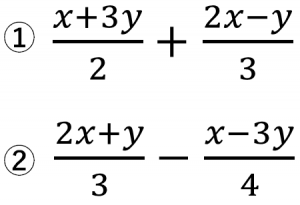



中2数学 式の計算 間違えやすい計算問題 4つのタイプ たけのこ塾 勉強が苦手な中学生のやる気をのばす




分数を含む多項式の計算 まなびの学園




分数の多項式の足し算や引き算 通分してからがポイントだ 中学や高校の数学の計算問題




多項式の掛け算 割り算と分配法則 代入計算のやり方 リョースケ大学




同類項をまとめる 分数 清水塾




多項式の計算応用 分数をふくむ式 教遊者




多項式と単項式の乗除 無料で使える中学学習プリント




文字式の計算 カッコ 分数を含む多項式 計算ドリル 問題集 数学fun




中学2年生 数学 式の計算 単項式の計算 乗法 除法 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
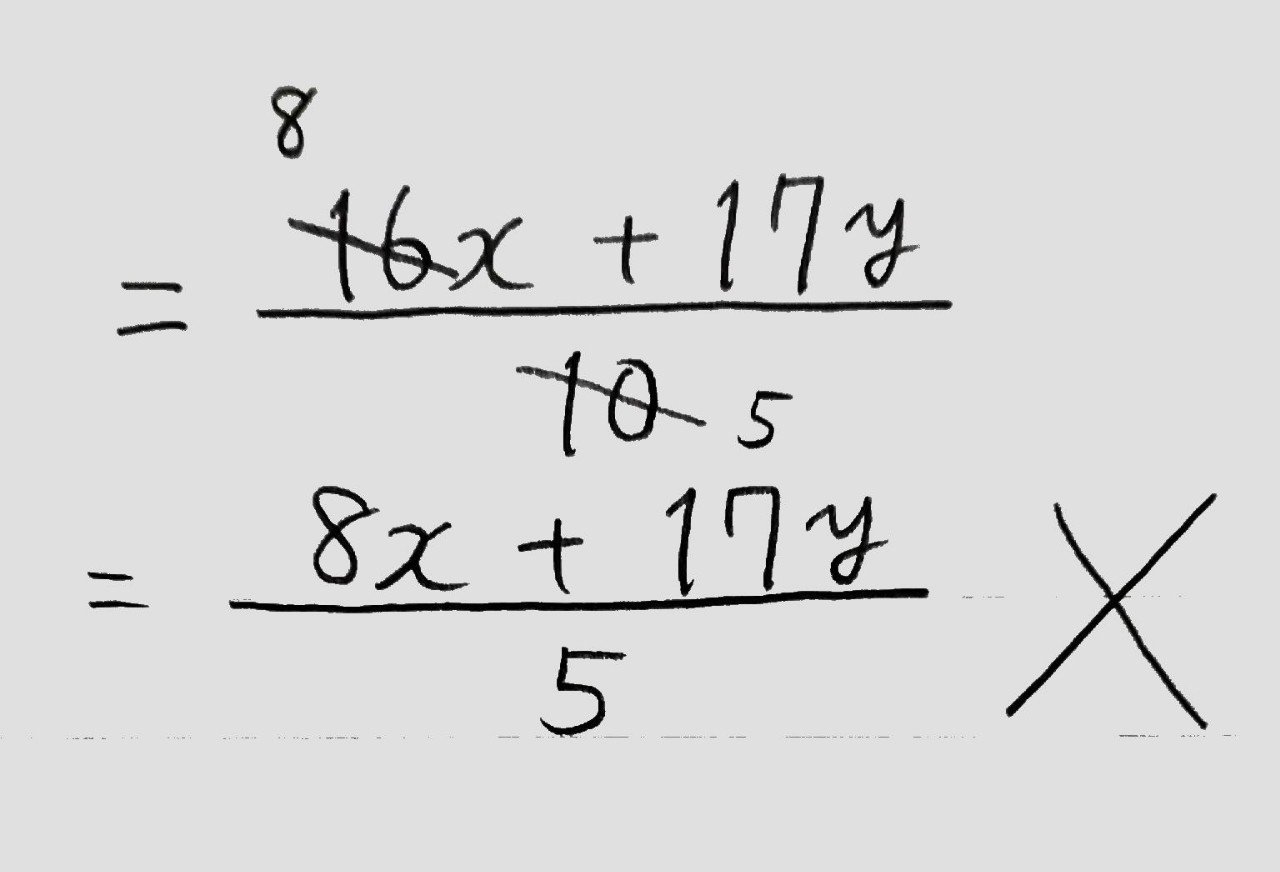



忙しい人のための中学数学 式の計算 計算ルール編 桜花 現役バイト塾講師 Note




Junior High数学的数学 小数 分数を含む計算 数検4級 筆記 Clear




多項式の計算応用 分数をふくむ式 教遊者




単項式の全てがこれでわかる 単項式の係数と次数 乗法 除法や多項式との違いまで 高校生向け受験応援メディア 受験のミカタ




方程式の問題で分数のときは分母を通分すべきなのか 中学や高校の数学の計算問題




数 学
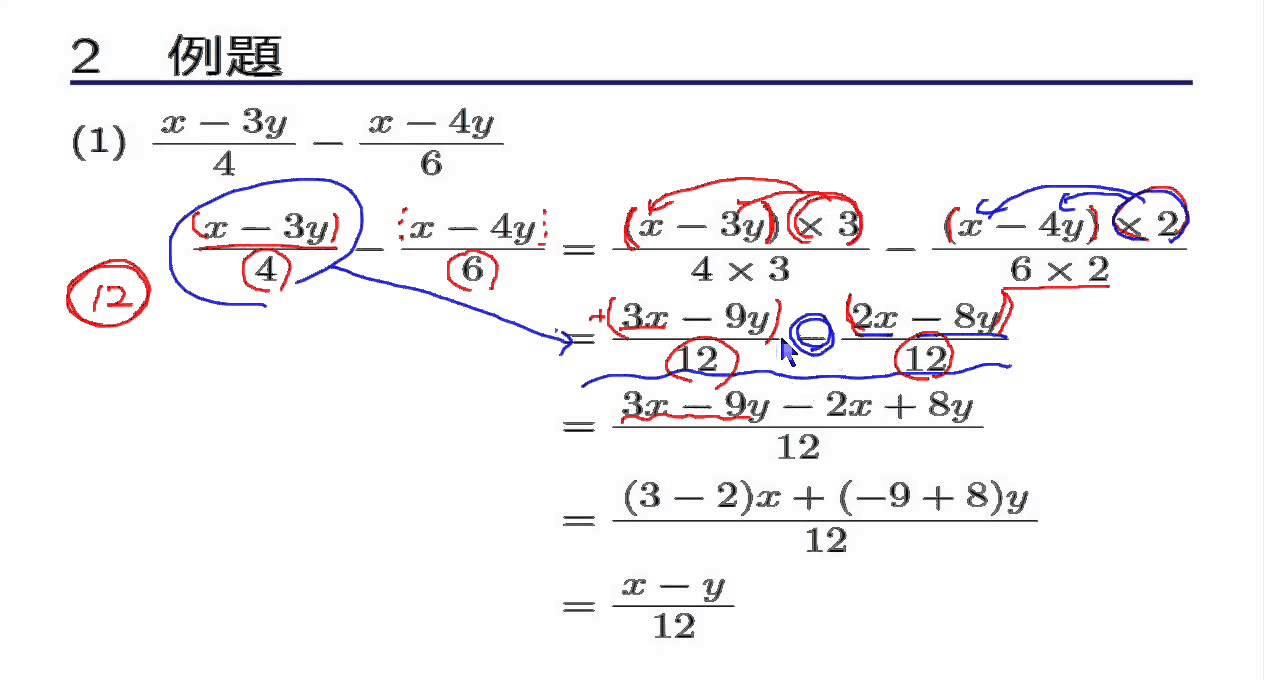



中2数学 式の計算 1 6 多項式の計算 分数 Youtube




中3 展開と因数分解3 多項式と単項式のいろいろな計算 予習 中学数学の勉強に




高校数学 関数の極限 多項式関数と分数関数の極限 受験の月




中2数学 多項式の計算のやり方についてイチから解説 中学数学 理科の学習まとめサイト




数学 中2 5 いろいろな多項式の計算 Youtube



2
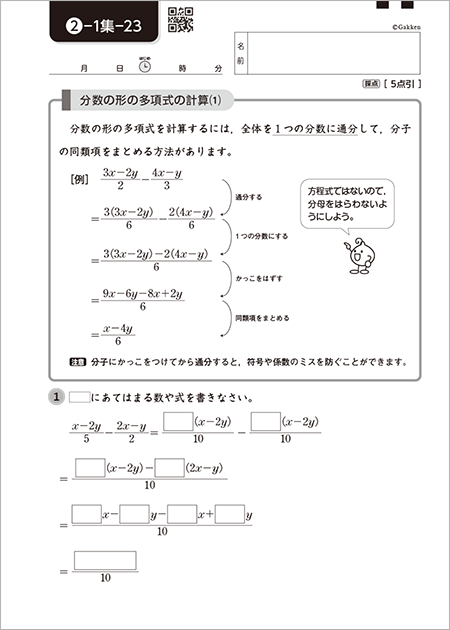



学研教室




多項式の加減法の応用問題 かっこの前がマイナスの問題がよく出る 中学や高校の数学の計算問題



0 件のコメント:
コメントを投稿